14.10.2024
O teorema de Tales é parte fundamental da geometria plana, entenda tudo sobre o assunto neste artigo!
Você vai encontrar aqui:
- O que é o teorema de Tales
- Conceitos básicos para entender a lei de Tales
- Como aplicar o teorema de Tales
- Aplicação do teorema de Tales nos triângulos
- Aprenda com esse vídeo um pouco mais da história de Tales de Mileto
- Precisa de ajuda com matemática?
- Revisão do teorema de Tales
- Exercícios resolvidos sobre o teorema de Tales
Idealizado pelo primeiro filósofo do ocidente, Tales de Mileto, o teorema de Tales é fundamental para compreensão de questões da segunda parte de geometria plana no ENEM. O teorema explora a proporcionalidade entre retas e segmentos de reta, sendo muito utilizado em questões que envolvem triângulos e retas paralelas.
Ao ler esse artigo, você entenderá todos os termos e procedimentos utilizados em questões que envolvem o teorema de Tales. Ter uma compreensão maior do assunto te ajudará a desenvolver o raciocínio lógico, ir melhor em suas provas de matemática na escola e em processos seletivos.
O que é o teorema de Tales
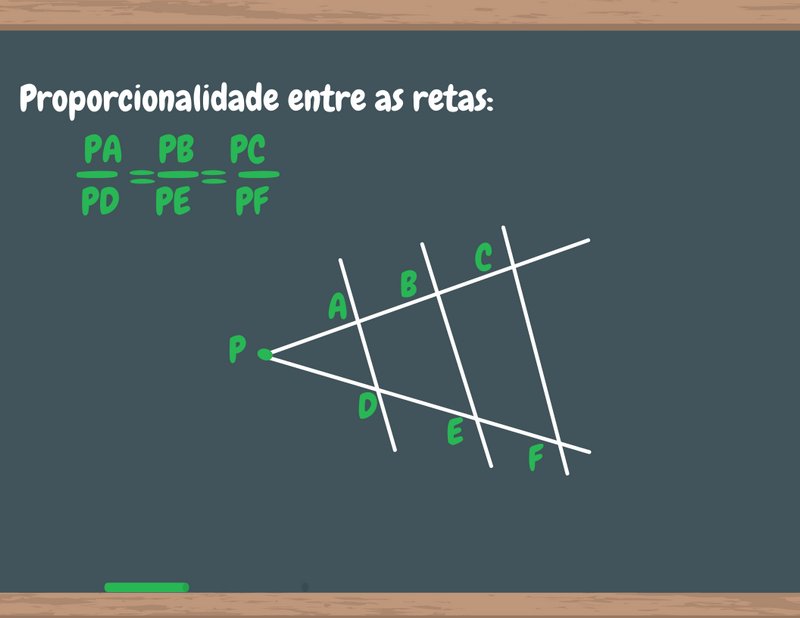
Saber aplicar o teorema de Tales em diferentes contextos irá facilitar a compreensão de questões de geometria plana nos vestibulares. Fonte: MyStudyBay
O teorema de Tales foi descoberto aproximadamente no ano 625 a.C. pelo filósofo, astrônomo e matemático, Tales de Mileto. A descoberta foi feita quando o pensador foi convidado pelo faraó para ir até o Egito, tendo assim a oportunidade de medir as pirâmides e suas sombras.
Relacionando os dados coletados, o pensador elaborou o teorema de tales: propriedade da geometria que confirma a existência de segmentos proporcionais quando há a sobreposição de retas paralelas cortadas por retas transversais.
Precisa de ajuda urgente com seu projeto?
Qualidade garantida, correções gratuitas em até 20 dias, pague agora ou em parcelas até 12 meses
Conceitos básicos para entender a lei de Tales
Para entender como aplicar a fórmula em questões que utilizem o teorema de Tales, é importante entender alguns dos conceitos fundamentais que são cobrados nas provas, como: retas paralelas, retas transversais e razão.
Feixes de retas paralelas
Para que dois segmentos de reta sejam considerados paralelos eles não devem se encontrar em nenhum ponto de sua trajetória. Para que isso seja possível, é básico que as retas devem ambas apontar na mesma direção (horizontal ou vertical) com inclinação de noventa graus.
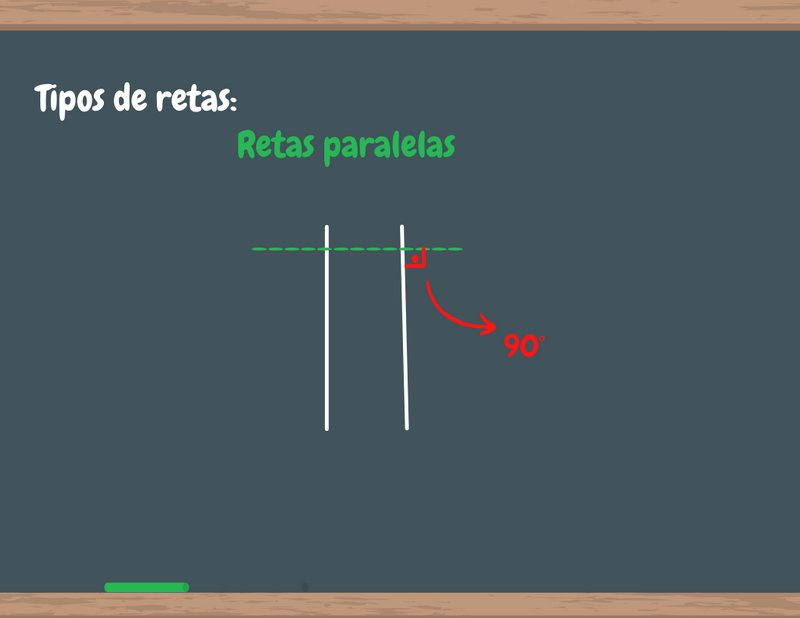
A imagem apresenta um resumo do que é um feixe de retas paralelas. Fonte: MyStudyBay.
Retas transversais
As retas transversais cortam as retas paralelas sendo fundamentais na relação de proporção no teorema de Tales. É possível identificar que uma reta pertence a essa classe ao verificar sua inclinação e direção, afinal, caso a reta cruze o mesmo ponto que outra, ela pode ser denominada como reta transversal.
Nesse caso, não há limitação quanto ao ângulo na denominação, contrário às regras de identificação de retas paralelas.
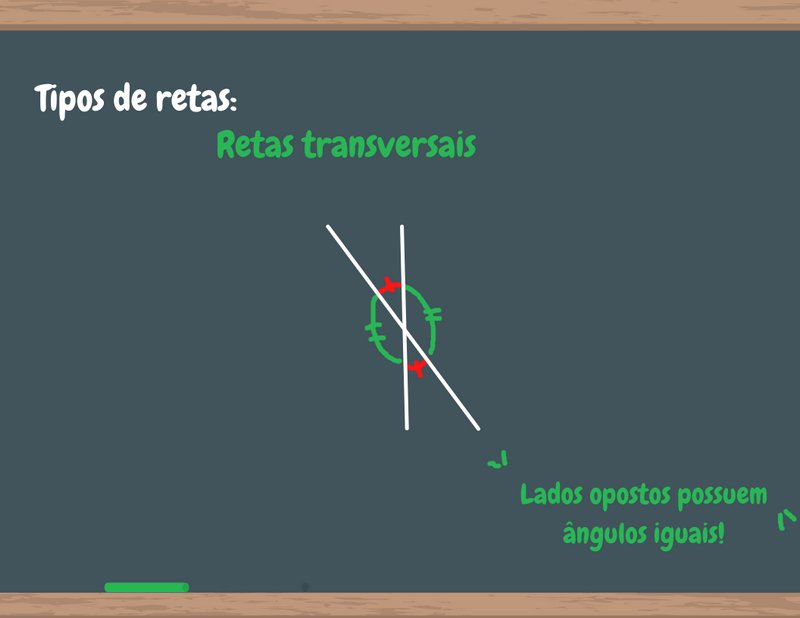
Os lados opostos de uma reta transversal são proporcionais, logo, possuem o mesmo valor. Fonte: MyStudyBay
Duas ou mais retas podem ser classificadas como transversais ao terem cruzado um ponto em comum com outra reta. Esse é um conceito fundamental para a interpretação da teoria de Tales.
Razão e proporção
Saber o conceito de razão e proporção é tão importante quanto saber reconhecer cada tipo de reta, para que você consiga aplicar calcular o valor de X no teorema de Tales.
O conceito de proporção é muito utilizado, desde a regra de três, até matérias que envolvem geometria ou porcentagem. Fonte: MyStudyBay
Como aplicar o teorema de Tales
Toda questão que envolva o teorema de Tales terá a presença de pelo menos dois feixes de retas paralelas e uma transversal, mesmo que a formação típica esteja escondida em um triângulo de Tales ou na projeção da sombra de um prédio.
A fórmula do teorema de Tales recai na relação entre as retas e resulta em segmentos proporcionais, que podem ser utilizados para descobrir valores desconhecidos a partir das relações estabelecidas.
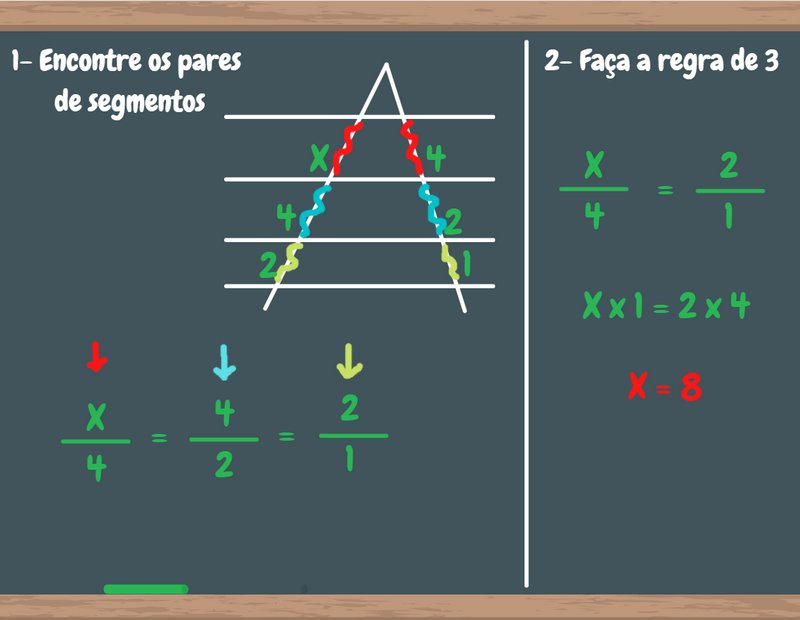
Explicação de como estruturar o cálculo utilizado em exercícios que envolvem a lei de tales. Fonte: MyStudyBay
O primeiro passo para resolver problemas com teorema de Tales é encontrar quais pares de segmentos foram formados. Para fazer isso marque os espaços formados entre os pontos atravessados pelas retas paralelas.
Em seguida, compare dois desses pares ordenados e realize a regra de três, assim, você conseguirá encontrar o valor da incógnita dentre os segmentos.
No caso do teorema de Tales com duas incógnitas, procure por um terceiro segmento que seja composto apenas de números e compare ele com as outras razões encontradas que possuem incógnitas.
Aplicação do teorema de Tales nos triângulos
A lei de Tales também pode ser aplicada em exercícios que envolvem triângulos. Veja a explicação para esse tipo de questão com o exemplo abaixo:
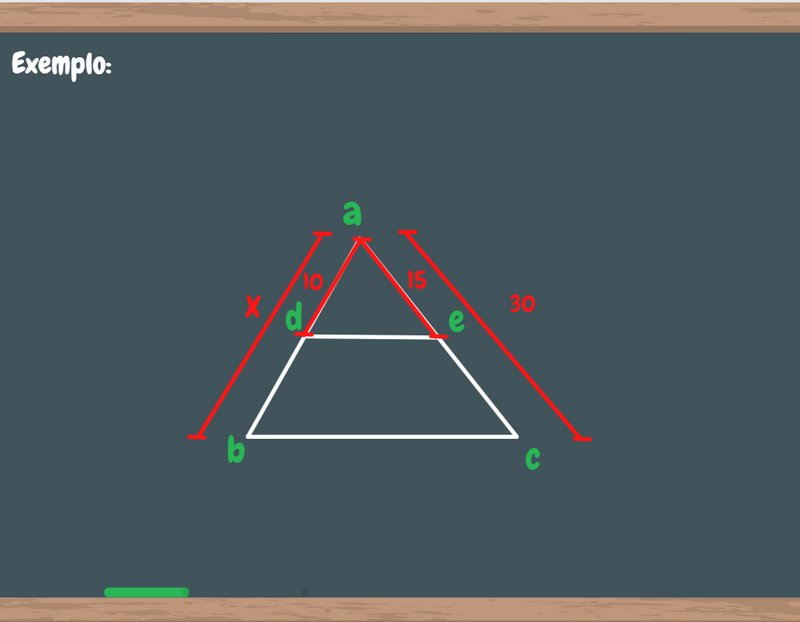
A imagem apresenta a aplicação do teorema de Tales Mileto em um exercício que envolve semelhança de triângulos. Fonte: MyStudyBay
Resolução passo a passo:
Aprenda com esse vídeo um pouco mais da história de Tales de Mileto
O vídeo explica detalhadamente a história do pai da geometria descritiva, Tales de Mileto. Todas as informações no vídeo possuem fundamento e são baseadas em fontes confiáveis citadas na descrição.
Precisa de ajuda com matemática?
Você por acaso é uma daquelas pessoas que se sente para trás quando se trata de matérias de exatas? Ou até mesmo um profissional buscando ajuda extra com trabalhos elaborados? Nós podemos te ajudar! Procure nossa equipe para receber auxílio com questões, exercícios e cálculos que parecem impossíveis de se aprender sozinho.
Somos uma empresa composta por profissionais treinados e experientes em preparar projetos de teor acadêmico, desde trabalhos escolares ao TCC. Nossa prioridade é garantir que você receba material original e de qualidade que você busca.
Precisa de ajuda urgente com seu projeto?
Qualidade garantida, correções gratuitas em até 20 dias, pague agora ou em parcelas até 12 meses
Revisão do teorema de Tales
Originado do antigo Egito, o teorema foi criado a partir da medição das pirâmides do Egito por parte de Tales de Mileto. A teoria serviu como base para muitas das teorias que conhecemos hoje, como o teorema de pitágoras.
A teoria é muito utilizada na vida real, por matemáticos, arquitetos e engenheiros. Isso é prova de que a matemática vai muito além do papel e tem utilidade real e aplicável no cotidiano, tornando-a uma matéria muito importante.
O teorema de Tales tem três conceitos principais a serem revisados:
- Retas paralelas
- Retas transversais
- Razão e proporção
Lembre-se de revisar o assunto para mantê-lo fresco em sua mente, caso você seja uma pessoa que gosta de se organizar, crie uma pasta no drive organizada por assunto e semestre com seus artigos e vídeo aulas favoritos, voltando sempre para revisar o conteúdo dado em sala de aula.
Exercícios resolvidos sobre o teorema de Tales
Utilize esses exercícios do ENEM para direcionar seus estudos.
Questão 1
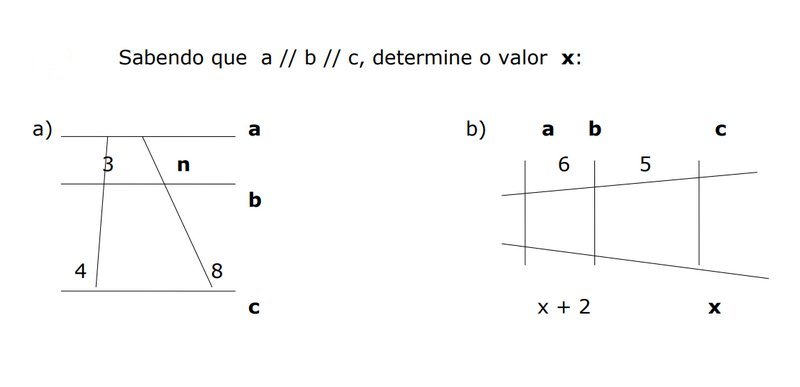
Questão 2
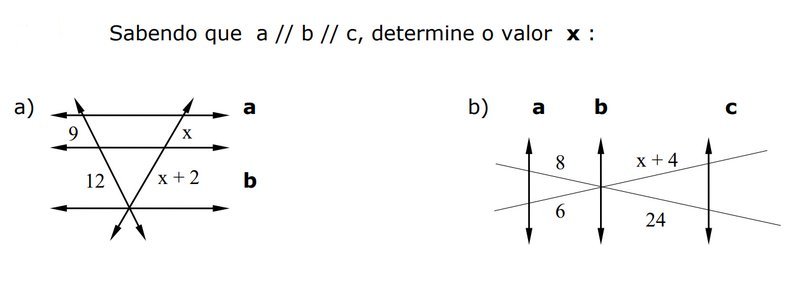
Respostas
Questão 1: n=6, x=10
Questão 2: x=6, x=28
Juliana N
Autora do Studybay
Meu nome é Juliana, sou Bacharel em Filosofia pela IFCH e pós-graduada em Instituto de Filosofia e Ciências Humanas da Unicamp. Tenho experiência grande com artigos, trabalhos acadêmicos, resumos e redações com garantia antiplágio.
