O estudo da Matemática é algo que encanta a alguns alunos e que assusta muitos deles devido à complexidade das discussões, a dificuldade dos exercícios e à abstração das teorias. Muitos alunos, ao se depararem com o tema fração geratriz nas aulas de matemática, podem ter dúvidas sobre o que se trata esse tema e como calculá-la de maneira simplificada. Pode parecer difícil a princípio, como tudo no estudo dos temas matemáticos, porém, com explicações detalhadas e com um pouco de dedicação, você tirará esse assunto de letra.
Tabela de Conteúdos
- Antes de começar, o que é uma dízima periódica?
- Definição de uma fração geratriz?
- Como encontrar uma fração geratriz da dízima periódica simples?
- E a dízima periódica composta?
- Confira neste vídeo: dízimas periódicas
- Você precisa de ajuda com seus trabalhos escolares?
- Compreender fração geratriz requer a compreensão da lógica e exercícios
- Perguntas mais frequentes quando o tema é fração geratriz
- Checklist na hora de calcular frações geratrizes
Neste artigo, vamos ajudá-lo a resolver essa preocupação de entendimento com explicações detalhadas sobre o que se trata a fração geratriz, para o que ela é importante em termos de equações e resolução de problemas, como ela é usada para se encontrar dízimas periódicas simples e dízimas periódicas compostas e vamos também fornecer alguns exemplos práticos no qual a compreensão será certamente garantida.
Antes de começar, o que é uma dízima periódica?
Para nos aprofundarmos no assunto da fração geratriz da dízima periódica, é importante antes relembrar do que se trata uma dízima periódica. Segundo a Plataforma Mundo Educação da Uol,
As dízimas periódicas são decimais infinitos que, a partir de alguma casa após a vírgula, passam a repetir determinada sequência de algarismos de forma infinita.
As dízimas periódicas, justamente por serem números infinitos, são sempre expressas com as reticências ao final dos números.
Temos, como alguns exemplos de dízimas, os seguintes valores:
4,555…
34,787878…
0,052634634…
Como é possível observar, no exemplo anterior, há repetições de determinados números após a vírgula. No primeiro caso, temos a repetição do "5", em seguida, a repetição é do "78" e, por fim, no último caso, vemos a repetição de "634". Cada sequência dessas é chamada de período. Os números anteriores ao período (e depois da vírgula) são chamados de antiperíodos.
A dízima que logo depois da vírgula inicia uma repetição de números é conhecida como dízima periódica simples. Percebe-se que ela não tem antiperíodos. Já aquela que tem um outro número anterior à repetição é conhecida como dízima periódica composta.
Avaliando os mesmos exemplos anteriores:
|
Dízima periódica |
Parte inteira |
Parte decimal |
Período |
Antiperíodo |
Classificação |
|
4,555… |
4 |
0,555... |
5 |
- |
Simples |
|
34,1787878… |
34 |
0,1787878... |
78 |
1 |
Composta |
|
0,052634634… |
0 |
0,052634634… |
634 |
052 |
Composta |
Toda dízima periódica pode ser transformada em uma fração, uma vez que é um número racional. Na próxima seção, vamos falar mais sobre a fração que origina as dízimas periódicas.
Definição de uma fração geratriz?
Uma fração geratriz, em termos gerais, pode ser explicada pela seguinte frase:
É uma fração cujo numerador dividido pelo denominador dá origem a uma dízima periódica.
Seguem alguns exemplos para análise:
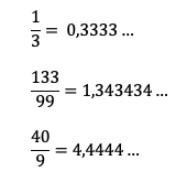
Dessa maneira, saber mais profundamente sobre frações geratrizes facilita (e muito!) na hora de resolver problemas em operações matemáticas básicas que envolvem as dízimas periódicas.
Como encontrar uma fração geratriz da dízima periódica simples?
Calcular a fração geratriz pode ser simples seguindo alguns passos básicos, apresentados a seguir:
- Separe a dízima periódica em uma soma de duas partes principais: uma em que haja apenas sua parte inteira e outra com a sua parte decimal.
- Conte quantos são os algarismos no período do número decimal. Isso vai definir, posteriormente, qual será o denominador.
- Para a parte decimal, formule uma fração em que o numerador é o período e o denominador tem todos os números iguais a 9 seguindo a quantidade de números do período.
- Transformar a parte inteira também em uma fração, multiplicando o valor pelo denominador já encontrado para a parte decimal.
- Somar as partes inteira e decimal em formato fracionário. Você terá como resultado a sua fração geratriz.
Vamos analisar o número 2,333... e encontrar sua fração geratriz:
- Passo 1) A parte inteira é 2; a parte decimal é 0,333…
- Passo 2) Um algarismo no período - o número 3.
- Passo 3) Como é apenas um algarismo no período, a parte de baixo da fração será formada pelo número 9.
![]()
- Passo 4) Multiplica-se a parte inteira 2 pelo 9 para ter esse número em formato de fração (18).
![]()
- Passo 5) Realizando a soma entre as duas frações, temos como resultado a fração geratriz:
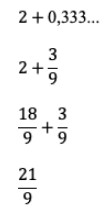
Vamos agora fazer a resolução de outro exemplo, dessa vez, vamos encontrar a fração geratriz do número 47,789789…
- Passo 1) A parte inteira é 47; a parte decimal é 0,789789…
- Passo 2) Três números no período - os números 789.
- Passo 3) Como são três cifras no período, a parte de baixo da fração será formada por três números 9.
![]()
- Passo 4) Multiplica-se a parte inteira 47 por 9 para ter esse número em formato de fração (46953).

- Passo 5) Realizando a soma entre as duas frações, temos como resultado a fração geratriz

E a dízima periódica composta?
O cálculo da dízima periódica composta, apesar de conter algumas particularidades, segue a mesma lógica do cálculo que vimos anteriormente com a dízima periódica simples. Tal como apresentamos anteriormente, vamos passar um passo a passo e mostrar alguns exemplos para compreensão da matéria apresentada.
|
Separe |
Separe a dízima periódica em uma soma de duas partes principais: uma em que haja apenas sua parte inteira e outra com a sua parte decimal. |
|
Contar |
Na parte decimal, contar quantos são os algarismos que estão no período e no antiperíodo. |
|
Escreva |
Escreva uma fração da parte decimal em que o numerador é formado pela subtração entre os algarismos não repetidos e os algarismos do antiperíodo. Se o número analisado é 7,65888… podemos dizer que sua parte decimal é 0,65888… e a fração a ser escrita será com a diferença do (658 - 65). Já o denominador vai ser composto por algarismos iguais a 9 (conforme a quantidade de algarismos do período) seguido de algarismos iguais a 0 (de acordo com a quantidade de algarismos do antiperíodo). No caso acima, teremos um 9 e dois 00 (900). |
|
Transformar |
Transformar a parte inteira também em uma fração, multiplicando o valor pelo denominador já encontrado para a parte decimal. |
|
Somar |
Somar as partes inteira e decimal. Você terá como resultado a sua fração geratriz. |
Exemplo:
Qual a fração que origina a dízima periódica composta 2,56333... ?
- Passo 1) A parte inteira é 2; número decimal é 0,56333…
- Passo 2) Um algarismo no período - o número 3 e duas cifras no antiperíodo (56).
- Passo 3) O numerador será formado subtração entre os algarismos não repetidos (563) e os algarismos do antiperíodo (56). Como é apenas um algarismo no período e duas cifras no antiperíodo, o denominador terá um número 900. Realiza-se a subtração e tem-se como diferença o número 507 no numerador e 900 no denominador dessa fração.
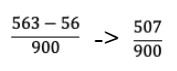
- Passo 4) Multiplica-se a parte inteira 2 pelo 900 para ter esse número em formato de fração (1800 no numerador e 900 no denominador).
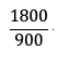
- Passo 5) Realizando a soma entre as duas frações, temos como resultado a fração geratriz:
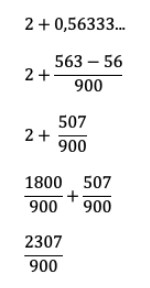
Vamos agora fazer outro exemplo, dessa vez, vamos encontrar a fração geratriz do número 4,123789789…
- Passo 1) A parte inteira é 4; o número decimal é 0,123789789…
- Passo 2) São três cifras no período (789) e três cifras no antiperíodo (123).
- Passo 3) O numerador será formado subtração entre as cifras não repetidas (123789) e as cifras do antiperíodo (123). Como são três algarismos no período e três algarismos no antiperíodo, o denominador terá um número 999000. Realiza-se a subtração e tem-se como diferença o número 123666 no numerador e 999000 no denominador dessa fração.
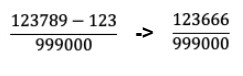
- Passo 4) Multiplica-se a parte inteira 4 pelo 999000 para ter esse número em formato de fração (3996000 no numerador e 999000 no denominador).

- Passo 5) Realizando a soma entre as duas frações, temos como resultado a fração geratriz:

Confira neste vídeo: dízimas periódicas
Você precisa de ajuda com seus trabalhos escolares?
Por acaso você ainda está com dúvidas sobre o tema da fração geratriz ou então precisa entregar um trabalho escolar e não tem tempo para se dedicar a ele? Sabemos que, às vezes, se torna praticamente impossível conciliar todas as demandas escolares e acadêmicas e uma ajuda parece ser o que mais necessitamos. Então você não precisa se preocupar mais, nós podemos ser essa ajuda para você!
Nossa equipe conta com um time de especialistas altamente especializados, com conhecimentos nas mais variadas áreas e experiência na elaboração de trabalhos escolares e acadêmicos. Fazemos desde redações e trabalhos escolares, passando pelos artigos acadêmicos, monografias, até chegar nas dissertações e teses.
Podemos fazer a sua atividade seguindo a sua necessidade de natureza do trabalho, prazo de entrega, tema, linha argumentativa, extensão em páginas e formatação (ABNT ou aquela definida pela sua instituição de ensino). Ao elaborar todos os nossos trabalhos a partir do zero, podemos garantir altíssima qualidade, total originalidade e aderência aos requisitos técnicos.
Não perca mais tempo, envie-nos um email com suas informações de contato e também com as especificações de seu trabalho para que possamos enviar uma proposta de valor que possa atender às suas necessidades.
Compreender fração geratriz requer a compreensão da lógica e exercícios
Assim como os demais temas dentro da Matemática, o conjunto de regras que compõem o tema das frações geratrizes requer que o aluno não apenas decore suas fórmulas e memorize a forma de fazer as operações. Esse método se mostra temporário e ineficaz dentro do processo de aprendizado.
A estratégia mais eficaz é compreender a lógica por trás do seu método e, a partir daí, o aluno ser capaz de fazer muitos exercícios. O treino constante propiciará a consolidação da compreensão e permitirá que o aluno não apenas aprenda esse tema, mas também que esteja preparado para os próximos desafios no campo da Matemática.
Porém, caso você tenha algum problema ou falta de tempo para se dedicar a seus trabalhos escolares ou acadêmicos, então não se esqueça de nos contactar.
Perguntas mais frequentes quando o tema é fração geratriz
Como fazer uma fração geratriz?
Para se encontrar uma fração geratriz, é necessário que o aluno diferencie se o que ele quer transformar em fração geratriz se trata de uma dízima periódica simples, ou seja, se o conjunto de números após a vírgula são iguais, ou então se ele está lidando com uma dízima periódica completa, em que há elementos diferentes antes da repetição. Para os casos simples, o cálculo terá como base a transformação dos valores em frações de denominador 9, 99, 999 (de acordo com a quantidade de períodos). Para os casos compostos, o cálculo será pautado na transformação dos valores em fração com base 9 e 0 ( de acordo com a quantidade de períodos e antiperíodos, respectivamente).
O que é fração geratriz e quais são seus exemplos?
Trata-se daquela fração que, quando fazemos a divisão efetiva entre os valores, encontramos um valor infinito com uma sequência repetida de valores. A fração 2/9 é um exemplo pois, quando realizamos a divisão do 2 pelo 9, temos o valor 0,222… Para fazermos equações e cálculos mais complexos, pode ser extremamente estratégico saber encontrar uma fração geratriz.
Checklist na hora de calcular frações geratrizes
Autora do Studybay
Meu nome é Juliana, sou Bacharel em Filosofia pela IFCH e pós-graduada em Instituto de Filosofia e Ciências Humanas da Unicamp. Tenho experiência grande com artigos, trabalhos acadêmicos, resumos e redações com garantia antiplágio.



















