26.01.2024
Sente que ainda não dominou a fórmula de Bhaskara? Então leia esse artigo, pois focamos em explicar de forma simples esse método de resolução das amadas equações do segundo grau. Entenda como fazer, veja alguns exemplos e pratique com nossos exercícios, para fixar melhor.
Você vai encontrar aqui:
- Equação do segundo grau e Bhaskara
- O que é a fórmula de Bhaskara
- Como aplicar a fórmula de Bhaskara em equação quadrática
- O que fazer e o que evitar
- Vídeo sobre a fórmula de Bhaskara
- Precisa de ajuda?
- Exercícios de equação de segundo grau com Bhaskara
- Resolva a equação a seguir, passo a passo: x² - 5 x + 6 = 0
- Perguntas frequentes sobre Bhaskara
Equação do segundo grau e Bhaskara
A equação de segundo grau se apresenta completa quando apresenta todos seus elementos nas contas: a incógnita elevada ao expoente 2 (quadrado), uma elevada a 1 e um algarismo sem incógnita. Quando incompleta, quaisquer desses termos podem não estar presentes.
Para ilustrar, ela é reconhecida da seguinte forma:
Segundo a teoria, toda equação do segundo grau pode ser resolvida com Bhaskara, mas essa não é a única forma. Há também a possibilidade de usar soma e produto, através de múltiplos e divisores. Porém, além de maiores chances de erro, por não ser tão estruturada quanto a fórmula de Bhaskara, torna-se extremamente cansativa, quando se trata de números decimais.
Ou seja, se você quer resolver uma equação do segundo grau, opte pelo teorema de Bhaskara, um método repetitivo, porém simples e funcional. A fórmula leva esse nome em homenagem ao matemático indiano que a criou. Entenda melhor como resolver logo a seguir.
O que é a fórmula de Bhaskara
Fonte: Unsplash
A equação de Bhaskara é simplesmente uma das mais conhecidas e utilizadas, tornando-se um dos cálculos fundamentais nos últimos anos escolares, vestibulares e ENEM. Em uma equação normal, não se faz necessária, mas quando se trata de uma quadrática, tem que estar presente. Afinal, ela torna tudo mais fácil e rápido de se calcular.
A lei de Bhaskara (ou fórmula de bháskara, você vai encontrar ambas as grafias), é feita para encontrar os termos faltantes, utilizando para isso a discriminante delta, que representa por si, um cálculo simples.
Veja como a fórmula é estruturada, dando sentido às equações:
Observe que logo após o -b, você encontra ambos os sinais, de soma e multiplicação. Isso acontece pois o cálculo será feito com as duas raízes da equação, positiva e negativa, que levam o resultado a zero. Veremos isso logo em breve, continue a leitura.
Como aplicar a fórmula de Bhaskara em equação quadrática
Para conseguir resolver sua equação do segundo grau, você precisa seguir alguns passos:
Todas as fórmulas que você vai precisar estão nesse card, que você pode salvar ou retornar ao site, sempre que quiser se lembrar.
Entenda cada um dos passos agora, em detalhes, para fazer o cálculo com a fórmula de Bhaskara resolvida e chegar ao resultado da equação. Para ficar mais fácil, vamos fazendo um exercício juntos, enquanto entendemos cada etapa. Para isso, tenha como base, a seguinte equação:
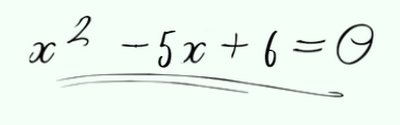
1. Ache a discriminante da equação
A discriminante da equação é um valor numérico resultante da soma dos valores apresentados. Também chamada de discriminante Delta, é muito fácil de achar e acaba baseando as raízes de uma equação. Veja a fórmula:
Ela está presente na fórmula de Bhaskara e deve ser calculada da seguinte forma, segundo o nosso exemplo anterior:
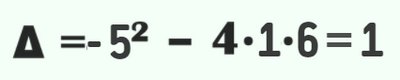
2. Substitua discriminante e coeficientes na fórmula de Bhaskara
Agora que você já sabe quem é Delta, basta substituir na fórmula de Bhaskara. Claro que também os coeficientes da equação devem ser substituídos pelos números correspondentes, facilitando assim o próximo passo, que é encontrar as raízes para determinar os valores que fazem com que a resposta seja zero.
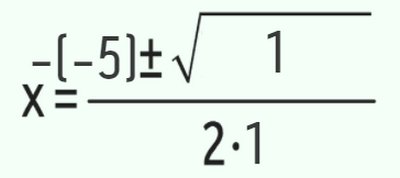
Muita atenção ao sinal inicial. Observe que b=-5 e, no início da fórmula, o sinal é negativo também. Assim, você deve manter o sinal e colocar o número negativo entre parênteses, multiplicando a seguir, antes de continuar a conta.
3. Calcule as raízes da equação
Você já tem a fórmula pronta, porém, observou que há ambos os sinais (+ e -) antes da raiz quadrada? Isso acontece pois ela está mostrando que há duas raízes, duas formas de resolver as equações, gerando assim dois coeficientes da equação, que são chamados de X’ e X’’ ou X1 e X2, a depender do professor. Veja como a fórmula é semelhante à de cima, porém uma das raízes é com soma e a outra com subtração:
Dessa forma, você terá dois resultados, que são as únicas duas equações que levam os valores a zero. Para não ficar nenhum grau de incerteza, vamos observar os valores na prática, alterando cada coeficiente pelo valor correspondente:
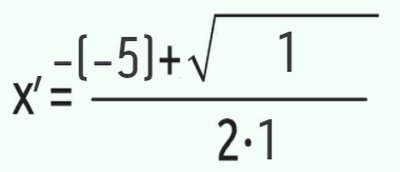
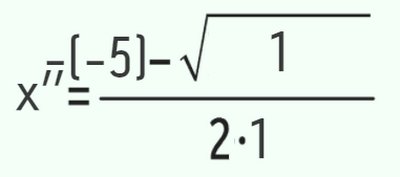
Na primeira fórmula, depois de trocados os coeficientes e feitos os cálculos, têm-se como resultado que X’=3 e X’’=2. Pronto, simples e prático. Agora, e se quiser ter certeza de que está certo? Basta fazer a prova real!
4. Prova real da equação do segundo grau
Quer ter certeza de que está realmente certa a sua conta? Fácil! Você sabe que em uma equação de segundo grau, a somatória é sempre igual a zero. Então, basta você substituir os termos, fazer o cálculo substituindo os coeficientes e confirmar o valor, que deve ser obviamente zero.
Lembrando que você tem duas raízes da equação que levam a esse valor, o X’ e o X’’. Faça o cálculo com cada um e saia da questão com a tranquilidade de quem tem certeza de que está certo!
O que fazer e o que evitar
Veja alguns pontos importantes que você deve fazer e evitar, quando estiver lidando com coeficientes, algum valor ou qualquer cálculo matemático em uma equação de segundo grau.
| O que fazer | O que não fazer |
|
|
|
|
|
|
|
|
Vídeo sobre a fórmula de Bhaskara
Conseguiu entender tudo? Para ajudar a fixar, assista a essa aula super-rápida, dando ainda mais sentido a tudo o que aprendeu aqui:
Precisa de ajuda?
Se você acha que um pouco mais de ajuda seria excelente, então pode contar com a Studybay! Nós podemos ajudar com todos os tipos de trabalhos em matemática, como TCCs em Matemática, Monografias, resolução de exercícios, cálculos, análises e muito mais.
Visite também o nosso Banco de trabalhos prontos na área Matemática, com exercícios propostos e resolvidos, aulas, slides e tudo o que você precisar para ter sucesso na sua jornada acadêmica. Se preferir, entre em contato agora pelo formulário e solicite o apoio dos nossos especialistas!
Precisa de ajuda urgente com seu projeto?
Qualidade garantida, correções gratuitas em até 20 dias, pague agora ou em parcelas até 12 meses
Exercícios de equação de segundo grau com Bhaskara
Agora, para fixar, faça os exercícios resolvidos abaixo e confira se a resposta está certa:
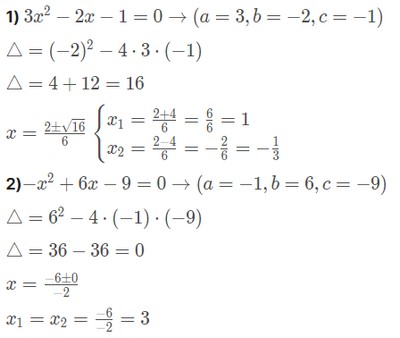
Fonte: Descomplica
Resolva a equação a seguir, passo a passo: x² - 5 x + 6 = 0
Perguntas frequentes sobre Bhaskara
Qual é a fórmula de Bhaskara?
A fórmula de Bhaskara é: x=-b²±√Δ / 2*1
Qual é a fórmula do Delta?
A fórmula do Delta é: Δ=b²-4*a*c
Angela Oliveira
Autora do Studybay
Redatora SEO, editora, proofreader e Copywriter sênior, amo explorar novos mundos, compartilhar ideias e saberes, através das palavras. Sou administradora habilitada e apaixonada por marketing, sempre em busca de novos desafios. Vamos crescer juntes? Fique à vontade para se conectar!
