Não seria muito absurdo ouvir queixas de algum aluno na aula de Matemática no momento de desvendar como calcular a mediana, a média e a moda. Isso porque esse assunto pode suscitar a dúvidas de como chegar a seus valores, confusão entre os seus conceitos e irritabilidade com possíveis equívocos. No entanto, trata-se de um assunto de suma importância na teoria matemática e na estatística.
Tabela de Conteúdos
- O que são medidas de tendência central na Estatística
- Média Aritmética
- Moda
- Mediana
- Alguns exemplos de cálculos de média, moda e mediana
- Precisa elaborar um trabalho e não sabe como começar? Nós podemos te ajudar!
- Vídeo sobre média, moda e mediana
- As medidas de tendências centrais nos ajudam a entender mais nossos dados
- As perguntas mais frequentes quando o assunto é mediana, moda e média
Neste artigo, vamos ajudá-lo a compreender como calcular essas medidas de tendência central, ou seja, como calcular a média, a mediana e a moda. Além disso, vamos compreender os seus usos e alguns exemplos para que o entendimento se torne mais fácil.
O que são medidas de tendência central na Estatística
As medidas de tendências centrais são cálculos usados para se compreender o comportamento de um conjunto de valores. A partir desses valores, é possível elaborar algumas pressuposições a respeito de uma série de números, podendo assim compreender melhor a natureza da mesma.
De acordo com a Wikipedia,
"(…) uma tendência central (ou, normalmente, uma medida de tendência central) é um valor central ou valor típico para uma distribuição de probabilidade."
As principais medidas são as seguintes:
- Média
- Moda
- Mediana
Nas próximas seções, vamos definir cada uma delas e apresentar a principal maneira de calculá-las.
Média Aritmética
A média apresenta vários tipos de cálculo, dentre elas a média aritmética, a média ponderada e a média geométrica.
A mais conhecida é a média aritmética, na qual é realizada a soma de todos os elementos de uma determinada sequência e, após isso, divide-se pela quantidade de elementos do grupo.
Exemplo: a média aritmética da série: 10, 15, 20 e 30 é de (10 + 15 + 20 + 30) / 4 . O resultado é igual a 18,75.
É importante dizer que a média funciona de forma mais efetiva em situações em que os valores da série não sejam muito discrepantes.
Exemplo: a média aritmética de uma série cujos valores são 1, 100 e 1000 é 367, o que diz pouco sobre os valores da série.
Moda
A moda diz respeito ao valor que tem mais frequência em uma determinada série de números. Neste caso, basta contar os elementos e suas repetições; o que aparecer mais equivalerá à moda do conjunto.
Por exemplo, no caso do conjunto formado pelos valores 70, 70, 70, 87, 90, 100, a moda é o número 70.
Mediana
A mediana é uma medida na qual se busca encontrar o número que se localiza na parte central de uma sequência, ou seja, quando encontramos o valor que divide na mesma quantidade o número de elementos à direita e à esquerda de uma série. É importante dizer que, para o cálculo da mediana se dar de forma correta, deve-se ordenar a sequência em ordem decrescente ou crescente.
Exemplo: no conjunto de dados 18, 20, 30, 65, 120 , observamos que a série já está organizada de forma crescente. Em seguida, podemos observar que há 5 valores, o que permite deduzir que há um número central. No caso, a mediana da série é o número 30.
Alguns exemplos de cálculos de média, moda e mediana
Nos exemplos a seguir, vamos avaliar alguns casos e calcular suas medidas de tendências centrais.
Sequência: 1 1 1 2 2 3 4 5 5 6 7 8 9 9 9 9 10
Essa série tem 17 elementos, está em ordem crescente e seu somatório dá 91.

| Média | Moda | Mediana |
| 91/17 = 5,3529... | 9 | 5 |
Sequência: 5 3 6 18 9 2 1 1 1
Essa série tem 9 elementos, não está em ordem crescente e sua soma dá 46.
Ordenando a série para se encontrar a mediana:
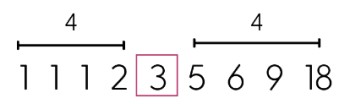
| Média | Moda | Mediana |
| 46/9 = 5,11111... | 1 | 3 |
Sequência: 189 90 7 543 2 62 2 2
Essa série tem 8 elementos, não está em ordem crescente e seu somatório dá 897. O problema aqui muda um pouco, pois a sequência tem um número par de elementos.
Ordenando a série para se encontrar a posição da mediana:
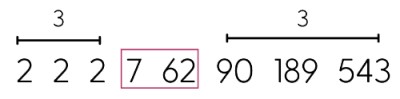
| Média | Moda | Mediana |
| 897/8 = 112,125 | 2 | (62 + 7) / 2 = 34,5 |
Precisa elaborar um trabalho e não sabe como começar? Nós podemos te ajudar!
Por acaso você precisa fazer um trabalho de estatística e você nem por onde iniciar a trabalhar com os dados? Ou então está sem tempo de fazer cálculos e elaborar um trabalho da forma que você deseja?
Então venha saber mais sobre a nossa empresa e nossos serviços de elaboração de trabalhos escolares e acadêmicos!
Nossa empresa é formada por um time experiente de profissionais que trabalham escrevendo trabalhos dos mais diversos tipos e propósitos. Podemos fazer desde redações e trabalhos para ensino fundamental e médio, até entregas acadêmicas como artigos, trabalhos de conclusão de curso, dissertações e teses. Seguimos as suas recomendações com relação a temas, prazos de entrega, extensão em páginas, linha de argumentação, formatação, garantindo alta qualidade e originalidade.
Então não espere mais: entre em nosso site e nos envie uma mensagem com seus dados de contato e informações sobre o trabalho a ser feito. Nossa missão é a de tornar a sua vida mais fácil e mais bem sucedida com os seus trabalhos escolares e acadêmicos.
Vídeo sobre média, moda e mediana
As medidas de tendências centrais nos ajudam a entender mais nossos dados
Encontrar a média, a moda e a mediana nos faz ter uma visão mais acurada de uma série de dados que estamos trabalhando. Talvez, para uma série menor de dados, não seja tão evidente o benefício dessas medidas. No entanto, para séries mais extensas em estudos complexos, esses valores são extremamente importantes para se iniciar a tecer conclusões sobre o comportamento da série e tomar ações a partir dele.
Portanto, nossa recomendação aos alunos é a de ter como objetivo treinar exaustivamente a trabalhar com essas medidas por meio de problemas e exercícios. Inicie com as séries mais simples e depois avance para as mais longas e extensas. A partir daí, enfim, você poderá progredir na análise de dados estatísticos.
As perguntas mais frequentes quando o assunto é mediana, moda e média
Como calcular o valor de uma mediana de um número par?
Basta encontrar os dois elementos centrais e fazer o cálculo de sua média aritmética simples. Vamos avaliar um exemplo de uma série que vai de 1 a 10 (10 elementos, ou seja, uma série com a quantidade de elementos sendo par): Os dois elementos centrais são os números 5 e 6. Tirando a média dos dois valores, encontramos o número 5,5, a sua mediana.
O que é valor mediano?
O valor mediano é aquele valor que se localiza no centro de uma série de elementos em uma sequência ordenada, seja de forma crescente ou decrescente. Ao encontrar uma mediana, sabemos que há a exata quantidade de valores do lado esquerdo e do lado direito da sequência.
Como calcular a mediana de uma tabela de frequência?
Essa tabela de frequência deve ser colocada em ordem crescente ou decrescente dos valores a serem calculados. A partir daí, basta encontrar o valor central (no caso de uma série com quantidade ímpar de elementos) ou então somar os dois elementos centrais e dividir por dois (no caso de uma quantidade par de elementos).
Como calcular a mediana de uma idade?
Para calcular essa medida, é necessário que seja apresentada toda a sequência de idades da pessoa. A mediana será o elemento central, ou seja, aquela que divide em duas metades as idades. Caso seja uma sequência com números pares, então basta pegar os dois elementos centrais, somá-los e dividi-los por dois. Vamos dar a seguir um exemplo com alguém que tem 9 anos: A mediana, neste caso, é de 5 anos.
Autora do Studybay
Meu nome é Juliana, sou Bacharel em Filosofia pela IFCH e pós-graduada em Instituto de Filosofia e Ciências Humanas da Unicamp. Tenho experiência grande com artigos, trabalhos acadêmicos, resumos e redações com garantia antiplágio.



















